Yetersiz verilere dayanarak erken teoriler oluşturmanın cazibesi mesleğimiz için ölümcüldür.
"Sherlock Holmes"
Yani Veri bilimcisi, verileri topladıktan sonra yazdığı programlar ile veriyi işleyip kullanılır hale getiren bir çeşit teknik analisttir.
Teori
Veri analizi mütemadiyen grafiklerden ve grafikler üzerindeki hesaplanmış verilerden oluşur. Lakin bu grafiklerde geçen her doğrusal düzlemin(verinin) bir denklemi vardır:
y = mx + c
Bu denklem nereden geliyor?
Aynı x ve y değerlerine sahip iki veri kümemiz olduğunu varsayalım:
Değerlerin grafikte çizilmesi şu şekilde olacaktır:
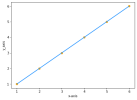
Peki y, x'e eşit olduğu için doğrumuzun denklemi y=x olacaktır, değil mi? Tabii ki Değil!
Grafiğe göre formülü hesaplarsak;
y=x matematiksel olarak y=1x ile aynıdır, veri biliminde ise bu oldukça farklıdır, doğrunun formülü y=1x olacaktır, burada 1, doğru ile x ekseni arasındaki açıdır, bu açı, doğrunun eğimi olarak da bilinir,
eğimi tanımlarsak,
eğim = y'deki değişim / x'deki değişim = m (eğim, m olarak ifade edilir. Eğim, grafikler arası kesişmedeki fiyat ortalamasıdır).
Formülümüz şimdi y = mx olacaktır.
Son olarak, denklemimize bir sabit eklememiz gerekiyor, bu, x sıfır olduğundaki y'nin değeridir, diğer bir deyişle doğru y eksenini kestiğindeki y'nin değeridir.
Sonuç olarak,
denklemimiz y = mx + c olacaktır (bu, veri biliminde bir modelden başka bir şey değildir),
burada c, y-kesimi yani x ile kesiştiği noktadaki korelasyondur.
Karmaşık Veriler
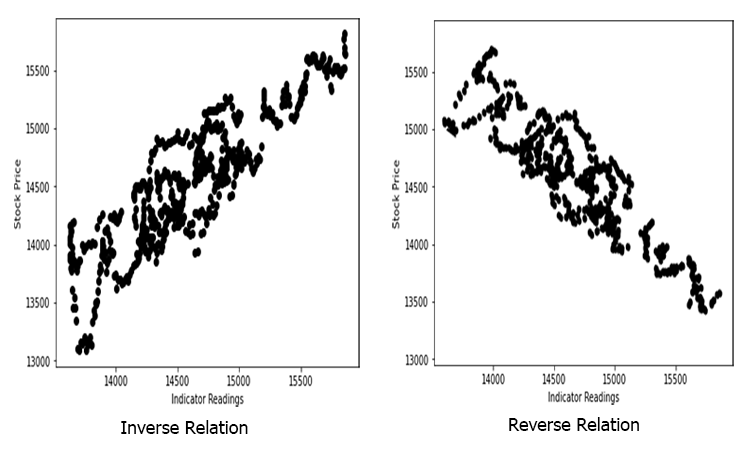
Hisse senedinin fiyatına göre gösterge değerlerini alıp grafikte çizdiğimizde aşağıdaki gibi rastgele dağılmış gösterge değerlerini elde ettiğimizi varsayalım (gerçek hayatta da durum böyledir).
Veri korelasyon uygulanması gereken ilk filtre, lineer modele dahil edilmemeleri adına hedefinizle yüksek düzeyde ilişkili olmayan tüm sütunları kaldırmaktır.
Lineer(doğrusal) olmayan ilişkili verilerle lineer bir model oluşturmak büyük bir temel hatadır; dikkatli olun!
İlişki ters olabilir ancak güçlü olmalıdır ve lineer ilişkiler aradığımızdan dolayı, bulmak istediğiniz şey de budur.
Peki, bağıntısız değişken ile hedefimiz arasındaki fiyatlamayı nasıl ölçeceğiz? Bunun için, korelasyon katsayısı olarak bilinen bir metrik kullanıyoruz.
Komut dosyasında NASDAQ ve S&P 500 kapanış fiyatlarını ve 50 periyotluk SMA (Basit Hareketli Ortalama), 13 periyotluk RSI değerlerini topladık. Verileri bir CSV dosyasında başarılı bir şekilde topladık, şimdi verileri Python'da Anaconda üzerinde Jupyter Notebook ile görselleştireceğiz. Makinelerinde Anaconda kurulu olmayanlar için bu yazıda kullanılan veri bilimi Python kodunu Google Colab'da çalıştırabilirsiniz.
Test komut dosyamız tarafından oluşturulan CSV dosyasını açmadan önce, Python tarafından okunabilmesi için onu UTF-8 kodlamasına dönüştürmeniz gerekir. CSV dosyasını not defteri ile açın ve UTF-8 kodlaması halinde kaydedin. Dosyayı dış dizine kopyalamak iyi bir şey olacaktır, böylece o dizine bağlanmak istediğinizde Python tarafından ayrı olarak okunacaktır, Pandas kullanarak CSV dosyasını okuyalım ve veri değişkeninde depolayalım.
RSI: Göreli güç endeksi (ing. relative strength index) finans piyasaların analizinde kullanılan bir teknik indikatördür. 1978 yılında J. Welles Wilder tarafından geliştirilmiştir ve ilk kez isimli kitabında yayınlanmıştır. RSI bir momentum osilatörüdür ve basitçe aşırı alım - aşırı satım sinyalleri üretir. Fiyatın yükselişindeki ve düşüşündeki dengesizlikleri ve bu dengesizliklerin normalleşme hızını ölçer.
Devamı gelecektir. Alıntı ve derlemedir.
"Sherlock Holmes"
Veri Bilimi ve Verilerin İşlenmesi
Yoğunlaşmış ve sınıflandırılmamış verilerden doğru sonuçlar elde etmek oldukça zorlu bir süreçtir. Bu süreçlerin işlemleri oldukça detaylı ve farklı formülleri birleştirmekten geçer. Çünkü verilerin ham haliyle karşımıza çıktığı durumlar onların bize tam da doğruyu söylemedikleri yerler olarak kabul edilir. Bilginin eyleme dönüştürülebilmesi için öncelikli olarak belirli süzgeçlerden geçirilmesi, uygun olan verilerin alınıp işlenmesi ve formüle edilmesi gerekmektedir. Aksi takdirde yanlış veriler işlenmeden, yanlış sonuçlar doğurabilir. Veri bilimcisi (analizcisi) önce verileri toplayıp sonrasında bunları formüle ederek doğru sonuca ulaşan ve bu sonuçlar doğrultusunda raporlar hazırlayıp şirketlere & devletlere istatiksel sunum yapan kişilerdir.Yani Veri bilimcisi, verileri topladıktan sonra yazdığı programlar ile veriyi işleyip kullanılır hale getiren bir çeşit teknik analisttir.
Lineer Regresyon (Korelasyon)
Bir bağıntılı değişken ile bir veya daha fazla bağıntısız değişken arasındaki lineer (doğrusal) ilişkiyi bulmak için kullanılan bir ön hesaplamalı yönteme Lineer Regresyon denir. Bu yöntem çok sık kullanılır çünkü modellemesi korelasyon alanındaki en basit sistemlerden birisidir. Temel de, verileri belirli bir lineer çizgide izleyip sonrasında ortalama hesaplaması ile en olası sonuçları ortaya koymaktadır. Algoritmaları da en çok kullanılan korelasyon türüdür.Model nedir?
Model dediğimiz sistem aslında sizin geliştirdiğiniz algoritmik bir veri analizi programından başka bir şey değildir.Teori
Veri analizi mütemadiyen grafiklerden ve grafikler üzerindeki hesaplanmış verilerden oluşur. Lakin bu grafiklerde geçen her doğrusal düzlemin(verinin) bir denklemi vardır:
y = mx + c
Bu denklem nereden geliyor?
Aynı x ve y değerlerine sahip iki veri kümemiz olduğunu varsayalım:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |

Peki y, x'e eşit olduğu için doğrumuzun denklemi y=x olacaktır, değil mi? Tabii ki Değil!
Grafiğe göre formülü hesaplarsak;
y=x matematiksel olarak y=1x ile aynıdır, veri biliminde ise bu oldukça farklıdır, doğrunun formülü y=1x olacaktır, burada 1, doğru ile x ekseni arasındaki açıdır, bu açı, doğrunun eğimi olarak da bilinir,
eğimi tanımlarsak,
eğim = y'deki değişim / x'deki değişim = m (eğim, m olarak ifade edilir. Eğim, grafikler arası kesişmedeki fiyat ortalamasıdır).
Formülümüz şimdi y = mx olacaktır.
Son olarak, denklemimize bir sabit eklememiz gerekiyor, bu, x sıfır olduğundaki y'nin değeridir, diğer bir deyişle doğru y eksenini kestiğindeki y'nin değeridir.
Sonuç olarak,
denklemimiz y = mx + c olacaktır (bu, veri biliminde bir modelden başka bir şey değildir),
burada c, y-kesimi yani x ile kesiştiği noktadaki korelasyondur.
Basit Lineer Regresyon
Basit lineer regresyon, bir bağıntılı değişkene ve bir bağıntısız değişkene sahiptir. Burada iki değişken arasındaki ilişkiyi anlamaya çalışıyoruz, örneğin bu, bir hisse senedi fiyatındaki değişimin SMA (Basit Hareketli Ortalama) ’daki değişimle olan ilişkisi olabilir.Karmaşık Veriler
Hisse senedinin fiyatına göre gösterge değerlerini alıp grafikte çizdiğimizde aşağıdaki gibi rastgele dağılmış gösterge değerlerini elde ettiğimizi varsayalım (gerçek hayatta da durum böyledir).
Bu durumda, göstergemiz/bağımsız değişkenimiz hisse senedi fiyatımızın/bağımlı değişkenimizin iyi bir veri görüntüleyicisi olmayabilir.
Veri korelasyon uygulanması gereken ilk filtre, lineer modele dahil edilmemeleri adına hedefinizle yüksek düzeyde ilişkili olmayan tüm sütunları kaldırmaktır.
Lineer(doğrusal) olmayan ilişkili verilerle lineer bir model oluşturmak büyük bir temel hatadır; dikkatli olun!
İlişki ters olabilir ancak güçlü olmalıdır ve lineer ilişkiler aradığımızdan dolayı, bulmak istediğiniz şey de budur.
Peki, bağıntısız değişken ile hedefimiz arasındaki fiyatlamayı nasıl ölçeceğiz? Bunun için, korelasyon katsayısı olarak bilinen bir metrik kullanıyoruz.
Korelasyon Katsayısı
Bu makalenin ana örneği olarak kullanılacak bir veri kümesi oluşturmak adına bir komut dosyası kodlayalım. NASDAQ için öngörücüleri bulalım.
Python:
input ENUM_TIMEFRAMES timeframe = PERIOD_H1;
input int maperiod = 50;
input int rsiperiod = 13;
int total_data = 744;
//+------------------------------------------------------------------+
//| Program Start |
//+------------------------------------------------------------------+
void OnStart()
{
string file_name = "NASDAQ_DATA.csv"; //--- Nasdaq Borsa Verisi
string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500";
//---
int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,",");
if (handle == INVALID_HANDLE)
{
Print("data to work with is nowhere to be found Err=",GetLastError());
}
//---
MqlRates nasdaq[];
ArraySetAsSeries(nasdaq,true);
CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq);
//---
MqlRates s_p[];
ArraySetAsSeries(s_p,true);
CopyRates(s_p500_symbol,timeframe,1,total_data,s_p);
//--- MA Verisi (Hareketli Ortalama)
int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE);
double ma_values[];
ArraySetAsSeries(ma_values,true);
CopyBuffer(ma_handle,0,1,total_data,ma_values);
//--- RSI Verisi
int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE);
double rsi_values[];
ArraySetAsSeries(rsi_values,true);
CopyBuffer(rsi_handle,0,1,total_data,rsi_values);
//---
if (handle>0)
{
FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI");
for (int i=0; i<total_data; i++)
{
string str1 = DoubleToString(s_p[i].close,Digits());
string str2 = DoubleToString(nasdaq[i].close,Digits());
string str3 = DoubleToString(ma_values[i],Digits());
string str4 = DoubleToString(rsi_values[i],Digits());
FileWrite(handle,str1,str2,str3,str4);
}
}
FileClose(handle);
}
//+------------------------------------------------------------------+
//| |
//+------------------------------------------------------------------+Test komut dosyamız tarafından oluşturulan CSV dosyasını açmadan önce, Python tarafından okunabilmesi için onu UTF-8 kodlamasına dönüştürmeniz gerekir. CSV dosyasını not defteri ile açın ve UTF-8 kodlaması halinde kaydedin. Dosyayı dış dizine kopyalamak iyi bir şey olacaktır, böylece o dizine bağlanmak istediğinizde Python tarafından ayrı olarak okunacaktır, Pandas kullanarak CSV dosyasını okuyalım ve veri değişkeninde depolayalım.
Genişletmek için tıkla ...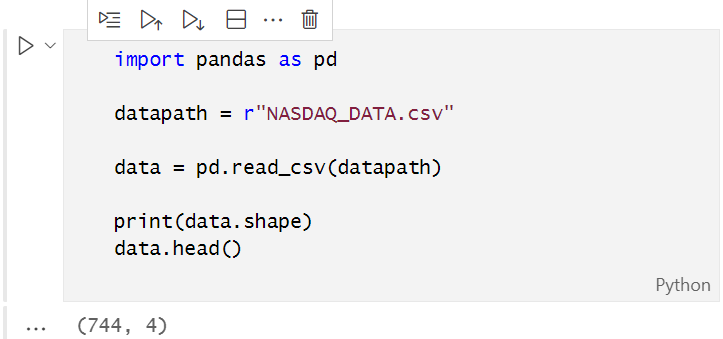
Genişletmek için tıkla ...
Çıktı aşağıdaki gibidir:Genişletmek için tıkla ...
Genişletmek için tıkla ...
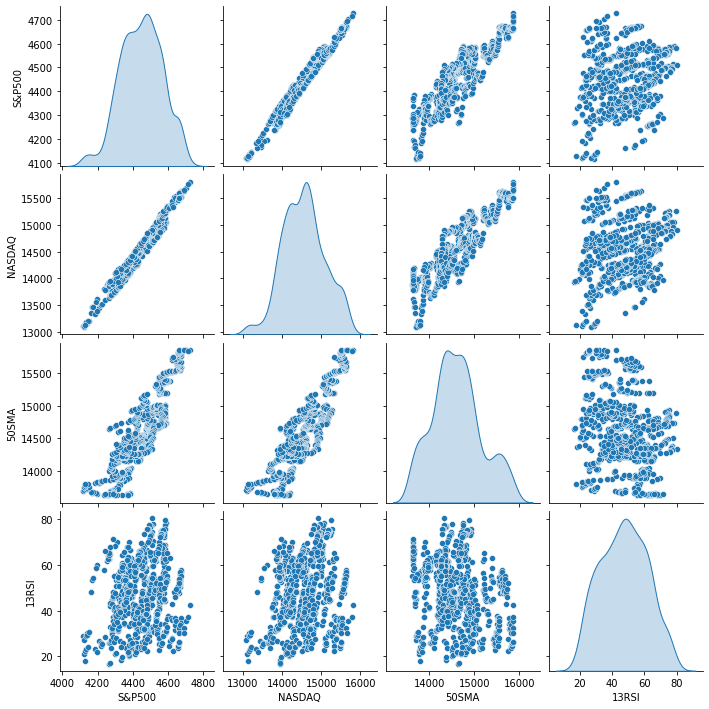
Verilerin görsel sunumundan, NASDAQ ile S&P 500 arasında çok güçlü bir ilişki olduğunu, NASDAQ ile 50 periyotluk SMA arasında da güçlü bir ilişki olduğunu görebiliyoruz. Daha önce de belirttiğimiz gibi, veriler grafiğin her tarafına dağıldığında, lineer ilişkiler bulmaya çalışıyorsak, bağımsız değişken hedefin iyi bir öngörücüsü olmayabilir. Ancak korelasyon konusunda sayıların söylediklerine bakalım, görsel olarak değil sayılara dayalı olarak sonuç çıkaralım. Değişkenlerin birbirleriyle nasıl ilişkili olduğunu anlamak adına korelasyon katsayısı olarak bilinen metriği kullanacağız.
RSI: Göreli güç endeksi (ing. relative strength index) finans piyasaların analizinde kullanılan bir teknik indikatördür. 1978 yılında J. Welles Wilder tarafından geliştirilmiştir ve ilk kez isimli kitabında yayınlanmıştır. RSI bir momentum osilatörüdür ve basitçe aşırı alım - aşırı satım sinyalleri üretir. Fiyatın yükselişindeki ve düşüşündeki dengesizlikleri ve bu dengesizliklerin normalleşme hızını ölçer.
Devamı gelecektir. Alıntı ve derlemedir.